Computational Fluid Dynamics
Depending on the problem definition, we have either used commercial third party software packages such as FLUENT, Fire Dynamics Simulator developed by NIST, or developed our own CFD packages. Two of our packages are:
MIFAC (Multiphase Internal Flow And Combustion), a Lagrangian code
MARS (Mixing And Reaction Simulation), a Eulerian code
Ansys FLUENT
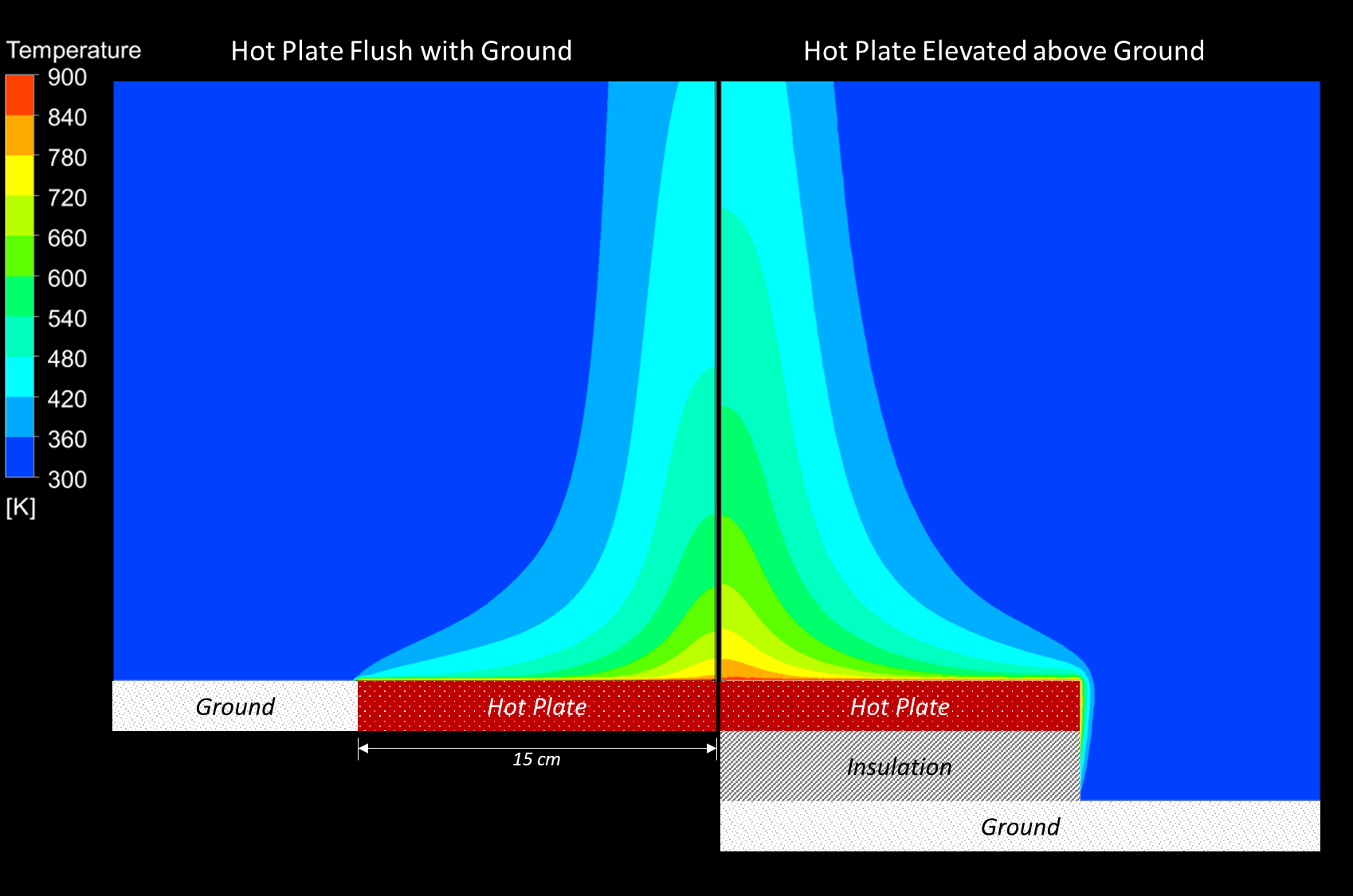
Ansys FLUENT's CFD package was used to compare the flow field around two configurations of a heated hot surface, one with the heated surface flush with ground and one with the heated surface elevated above ground. Because of symmetry only half plates are shown. Two half plates are placed side by side for easy comparison. The hot surface has a temperature of 630° C and develops a plume through natural convection. The temperature contours, velocity contours, and velocity vectors show that there is a difference between the two setups, mainly because the elevated hot surface has more surface area exposed to the ambient air, which results in higher temperatures and velocities.
FDS
Fire Dynamic Simulator (FDS) was used to analyze smoke movement in a test room. Smoke puffs is generated by intermittent combustion of liquids. The simulation was used to understand the reason for smoke escaping the exhaust hood. From the two gifs below, the effect of quiescent conditions was observed (left) and compared with a case where flow through the room door on the right wall is allowed (right). The buoyant plume becomes unstable when there is an external flow, pushing the smoke puffs outside the exhaust hoods edge. The results from this analysis was used to improve testing method.


MIFAC
MIFAC is an in-house Computational Fluid Dynamics Code (CFD) which uses a three-dimensional, fully-elliptic, finite difference representation of the steady-state conservation equations of mass, momentum, and energy. Turbulence is modeled using the k-epsilon equations. Gas-phase chemistry is also modeled using elliptic control-volume techniques. Particle dynamics are tracked using Lagrangian methods. Chemical kinetics calculations such as NOx formation (Zeldovich mechanism) are available using a post-processor elliptic solver linked to Chemkin-II, a gas-phase chemical kinetics package.
Results from modeling the Low NOx Burner
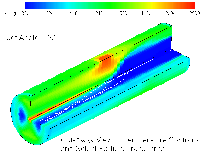
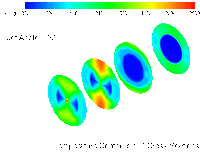
Configuration 1
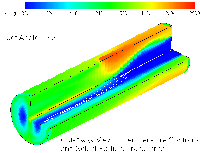
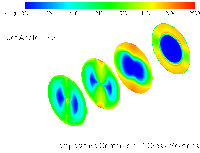
Configuration 2
CFD using the MARS Numerical Code
MARS (Mixing and Reaction Simulation) is a numerical code under development at BlazeTech based on the Lagrangian Vortex Element Method. This scheme uses the Navier-Stokes equations for incompressible viscous flow formulated in terms of velocity and vorticity variables. The flow field (vorticity field) is represented by a number of Lagrangian vortex elements. Each element is characterized by a position vector, a strength vector, and a radius. The fluid velocity at any location can be decomposed into two components: vortical and potential. The vortical component of the velocity is calculated by the superposition of the induced velocity from all the vortex elements using the Biot-Savart law. The potential velocity component can be obtained by solving the Laplace equation subjected to zero normal flow at any boundary surface. The viscous diffusion is included by the Random Walk Technique, with a velocity related to molecular viscosity and local subscale viscosity. No slip boundary conditions are satisfied by generating vortex sheets at the solid boundaries. The boundary condition at infinity is satisfied automatically.
Among its many advantages, this methodology is grid free and well suitable for transient problems. It is superior to existing Euler techniques for unsteady, high Reynolds number flows where it has an inherent ability to sense the onset of an eruptive event and respond quickly to concentrate computational resources (elements) into the erupting region.
Previous work has included the solution of unsteady, two dimensional, turbulent flow such as free jets, the rise of a hot, buoyant cloud in the atmosphere, and flow over a pitching and impulsively started airfoil. Two-dimensional solutions can be obtained on a Pentium PC.
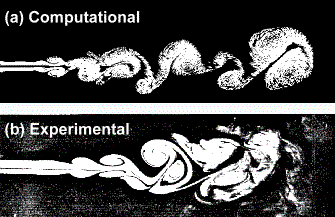
A snapshot of a starting, two-dimensional jet with a Reynolds number = 1500.
(a) BlazeTech computational results using vortex method and fast summation method,
(b) experimental measurements courtesy of S.Gogineni and C. Shih, FAMU/FSU College of Engineering.
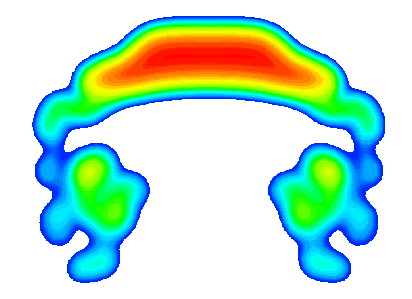
BlazeTech computational results of a hot, rising puff exhibiting the well-known mushroom shape.

Computational results courtesy of Szu-Chuan Wang using the Vortex Method for an impulsively started NACA 0012 airfoil at attack angle = 30° and Re = 5000 for various times (time step = 0.04).
Practical potential applications include aircraft noise prediction and control, simulation of coal combustion systems, aerodynamic analysis of airfoil geometry in unsteady flow, prediction of surface pressure fluctuations in turbulent flows, and many other unsteady, turbulent flow applications.
Current and future work involves the extension of MARS to three dimensions, adding compressibility effects, and modifying the conventional, direct computation of N-body interactions (operations proportional to O(N2)) with a fast summation scheme which reduces operations to O(N⋅logN).
